Ostatnia aktualizacja 3 kwietnia, 2023
Ciąg Fibonacciego to jedna z najbardziej znanych sekwencji matematycznych. Jest fascynująca ze względu na swoją prostotę i liczne zastosowania w różnych dziedzinach, od teorii liczb po biologię i ekonomię. Wielu z nas to zagadnienie poznawało już w szkole podstawowej, jednak czy wiesz, iż ciąg Fibonacciego spotykasz na co dzień, a sekwencję tę wykorzystują dziś choćby ogromne korporacje?
Zależności w ciągu Fibonacciego
Ciąg Fibonacciego to ciąg liczb naturalnych, w którym każdy kolejny element jest sumą dwóch poprzednich. Sekwencja zaczyna się od liczb 0 i 1, a zgodnie z zasadą, kolejne liczby są wyliczane ze wzoru.
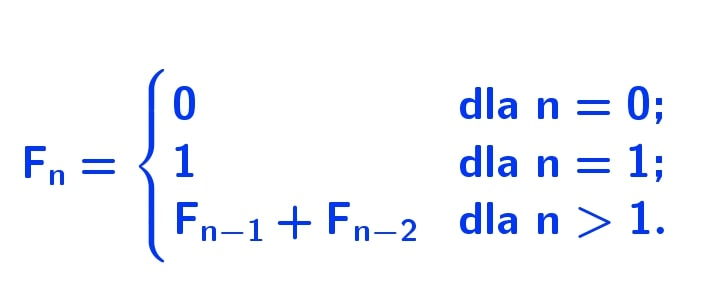
Pierwsze wyrazy ciągu Fibonacciego to zgodnie z powyższym:
F 1= 1,
F2 = 0+1 = 1
F3 = 1+1 = 2
F4 = 2+1 = 3
F5 = 3+2 = 5
F6 = 5+3 = 8
F7 = 8+5 = 13
F8 = 8+13 = 21
F9 = 13+21 = 34
F10 = 34+21 = 55
…
Jak widać, liczby w ciągu Fibonacciego powstają w sposób rekurencyjny, a więc każda kolejna liczba zależy od poprzednich.
Od królików do złotej proporcji
Nazwa “ciąg Fibonacciego” pochodzi od włoskiego matematyka Leonarda da Pisy, znanego także jako Fibonacci, który opisał go w swojej książce “Liber Abaci” w 1202 roku. Do odkrycia ciągu Fibonacciego przyczyniło się przeprowadzone przez autora badanie hodowli królików. Zadanie polegało na obliczeniu liczby par królików, które mogłyby być wyhodowane z jednej pary w ciągu roku. Fibonacci założył, iż każda para królików rodzi co miesiąc nową parę, a nowo narodzone pary dojrzewają i rodzą kolejne pary po dwóch miesiącach.
Jak się okazało, powstały w ten sposób ciąg, ma wiele interesujących własności. Jedną z nich jest to, iż każda liczba w ciągu jest równa sumie dwóch liczb poprzedzających ją. Co więcej, im dalej idziemy w ciąg, tym bardziej stosunek dwóch kolejnych liczb zbliża się do stałej wartości (1,618) zwanej złotą liczbą, boską proporcją lub złotym podziałem.
Złotą liczbę uzyskamy też np. dzieląc odcinek na dwie części w taki sposób, by stosunek długości dłuższej części do krótszej był równy stosunkowi całego odcinka do dłuższej jego części.
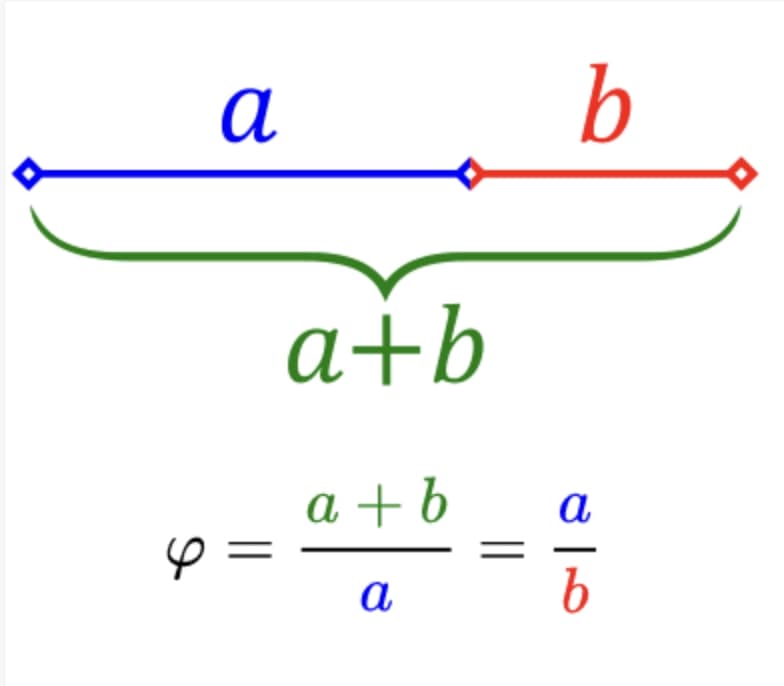Źródło: stormit.plZłota liczba, oznaczona symbolicznie grecką liczbą phi (φ), występuje w wielu dziedzinach matematyki, nauk przyrodniczych, sztuce i architekturze. Jest uważana za proporcję, która jest szczególnie estetyczna dla oka ludzkiego. W architekturze wiele budowli, zwłaszcza z okresu renesansu, zostało zbudowanych z wykorzystaniem złotej proporcji, co nadaje im harmonijny wygląd.
Ciąg Fibonacciego w przyrodzie
Ciąg Fibonacciego, oprócz swojego matematycznego znaczenia, jest obecny także w przyrodzie i zjawiskach naturalnych. Liczby ciągu Fibonacciego często pojawiają się w proporcjach, układach, kształtach i wzorach występujących w przyrodzie, co wskazuje na fundamentalną rolę, jaką odgrywają w jej strukturze i funkcjonowaniu.
Najbardziej znane przykłady występowania ciągu Fibonacciego w przyrodzie to:
- Rozmieszczenie liści na łodygach roślin.
- Rozmieszczenie nasion w owocach.
- Kształt pąków kwiatowych.
- Układ nasion w kłosach zbóż.
Co więcej, w proporcjonalnie zbudowanym ludzkim ciele, również doszukać się można zależności i liczb z ciągu Fibonacciego np. w stosunku odległości między stawami. jeżeli chodzi o ludzkie ciało, z zasadą złotej proporcji w osiągnięciu piękna, zgadzają się także lekarze medycyny estetycznej.
Ciąg Fibonacciego w XXI wieku
Na przestrzeni lat ciąg Fibonacciego znalazł wiele praktycznych zastosowań w dziedzinach sztuki, architektury i nauki. Jego śladów nie brakuje także w najnowszych rozwiązaniach technologicznych i biznesowych.
Stosowanie złotej proporcji pozwala między innymi na uzyskanie estetycznego wyglądu elementów graficznych. Zasadę ciągu Fibonacciego wykorzystały w tworzeniu logo marki, które z pewnością znasz. Między innymi:
- Pepsi,
- National Geographic,
- Toyota,
- Bp.
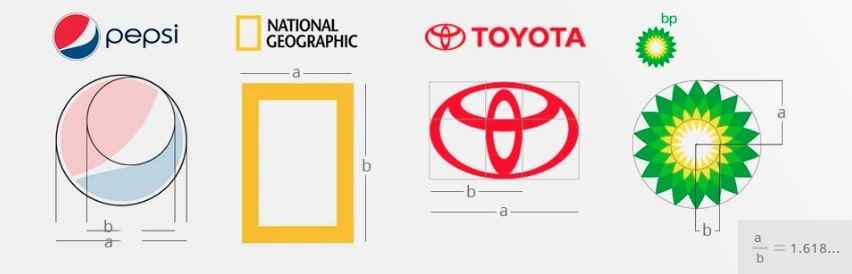Źródło: solveit.plCiąg Fibonacciego stosowany jest także w projektowaniu interfejsów użytkownika, na przykład do określenia proporcji między elementami interfejsu, takimi jak przyciski, ikony i pola tekstowe.
Zobacz: UI Design – czym jest? Jakie są wytyczne projektowania?
Popularna sekwencja matematyczna ma również zastosowanie w informatyce, gdzie jest wykorzystywana w algorytmach sortowania, kodowaniu czy sztucznej inteligencji. Ciąg Fibonacciego wykorzystuje się między innymi w uczeniu maszynowym. Pomaga w przewidywaniu wzorców i trendów w danych, a także w tworzeniu skomplikowanych modeli matematycznych, które pomagają w analizie danych i podejmowaniu decyzji. Przykładowo, można wykorzystać ciąg Fibonacciego do uczenia maszynowego do analizowania zmian cen w danym rynku.
Algorytmy oparte na ciągu Fibonacciego są wykorzystywane również w finansach, a konkretnie w analizie technicznej na rynkach finansowych. Temat analizy finansowej oraz zniesień Fibonacciego szerzej omawia film od FxMAG.
Jeśli zastanawiasz się, gdzie jeszcze znaleźć możesz złote proporcje, naprawdę nie musisz szukać daleko. Spójrz na swoją kartę płatniczą czy wyjątkowo elegancki samochód na ulicy. Czy, jak uważał Fibonacci, matematyka nie jest obecna w każdym aspekcie naszego świata?
