– Tato, co tam robisz na komputerze? – zapytała Jagódka.
– Wybieram optymalne zmienne do modelu i muszę troszkę przy tym pomysleć – odpowiedziałem.
– Heeee??? – dziwnie spojrzała się na mnie Otylka.
– Wyobraźcie sobie, iż pakujemy się na wakacje i możecie zabrać ze sobą jakieś zabawki (a same wiecie, iż macie ich bardzo dużo). Macie różne opcje to wyboru. Możecie na przykład spakować zabawki do małego plecaczka, który weźmiecie ze sobą do samolotu.
– Ale tam się zmieści mało zabawek! – gwałtownie zauważyła Jagódka.
– Zgadza się. Jest ich mało i po jakimś czasie wszystkie mogą Wam się znudzić, więc nie będziecie miały się czym bawić, ale za to łatwo je przewieźć. Możecie też spakować większą dodatkową torbę, ale za to trzeba będzie zapłacić i wtedy na miejscu kupimy mniej słodyczy. Oti się skrzywiła słysząc, iż na urlopie mogłoby mieć mniej słodyczy.
– Możecie też wziąć wszystkie zabawki, ale wtedy zamiast samolotem pojedziemy autkiem i podróż, zamiast trwać dwa filmy o krainie Lodu może zająć cały dzień i całą noc! A poza tym na miejscu i tak nie będziecie miały czasu wszystkim się bawić!
– O nie! To my idziemy pomyśleć, co będzie najlepsze. Chodź Oti, idziemy wybierać zabawki na wyjazd.
Wybór zmiennych to jedna z podstawowych koncepcji w uczeniu maszynowym, która ma ogromny wpływ na wydajność modelu. Każdy z nas budując model stanął przed problemem jak wybrać cechy do modelu.
W tym poście pokażę Ci najróżniejsze techniki, które możesz wykorzystać do wyboru modelu. Mam nadzieję, iż nie rozczaruję Cię mówiąc, iż nie ma złotego środka. Natomiast daję Ci ten arsenał, abyś z niego korzystał i eksperymentował.
Czym jest Feature Selection (wybór zmiennych)?
Wybór zmiennych (lub cech) to proces, w którym wybieramy te cechy w naszych danych, które mają największy wpływ na zmienną przewidywaną. Posiadanie nieistotnych zmiennych w danych może zmniejszyć dokładność wielu modeli, zwłaszcza algorytmów liniowych, takich jak regresja liniowa i logistyczna.
Innymi słowy, feature selection to proces wybierania podzbioru zmiennych z wszystkich przygotowanych dostępnych danych, aby uzyskać jak najlepszy model.
Dlaczego to jest ważne?
Oczywiście możesz się zatrzymać i zadać sobie proste pytanie: dobra, ale dlaczego nie przeliczać modelu na wszystkich danych? Przecież dobierzemy hiperparametry i model sobie poradzi.

Jest kilka istotnych powodów, dlaczego nie warto tego robić w ten sposób:
- Overfitting – jeżeli okaże się, iż mamy stosunkowo dużo cech w stosunku do liczby obserwacji, to model bardzo prosto będzie w stanie idealnie dopasować się na danych treningowych do funkcji celu. Natomiast takie podejście nie da nam uogólnionego modelu, a to jest naszym celem.
- XAI – im więcej zmiennych w modelu tym trudniej będzie nam wyjaśnić biznesowi, jak działa dany model. jeżeli możemy sobie pozwolić, zamiast 500 cech wdrożyć jedynie 20 kosztem niewielkiego spadku mocy, to pomyśl jak to ułatwi zrozumienie modelu!
- Większa dokładność – tutaj działa jedna z moich ulubionych zasad: „Shit in shit out”. Jeśli budując zmienne wykorzystamy automatyczne narzędzia jak np. featuretool, to większość stworzonych zmiennych nie będzie niosła żadnej informacji do modelowanego zagadnienia. A niska jakość danych wejściowych spowoduje powstanie modelu o niskiej jakości. Zatem pamiętaj: mniej mylących danych oznacza lepszą dokładność modelowania!
- Skraca czas treningu – bez zbędnej filozofii: mniej danych oznacza, iż algorytmy trenują szybciej.
- Ułatwia wdrożenie i utrzymanie – często zapominamy, iż sama budowa to jedno, ale wdrożenie i utrzymanie modelu to drugie. Im mniej cech tym ten proces będzie prostszy.
Mam nadzieję, iż również czujesz, iż wybór zmiennych to istotny temat i nie warto go pomijać!
Jak podzielić algorytmy do feature selection?
Istnieje wiele sposobów na wybór zmiennych (przekonasz się o tym w dalszej części wpisu). Natomiast większość tych metod możemy podzielić na trzy główne kategorie:
A. Oparte na filtrach (Filter methods)
Ostateczną listę charakterystyk filtrujemy na podstawie przyjętej metody. Może to być np. współczynnik korelacji Pearsona zmiennej z przewidywaną wartością. Metody te opierają się na cechach danych i nie używają algorytmów uczenia maszynowego. Zwykle są one szybsze kosztem niższej wydajności względem pozostałych metod.
 https://www.analyticsvidhya.com
https://www.analyticsvidhya.comB. Oparte na osadzeniach (embedded methods)
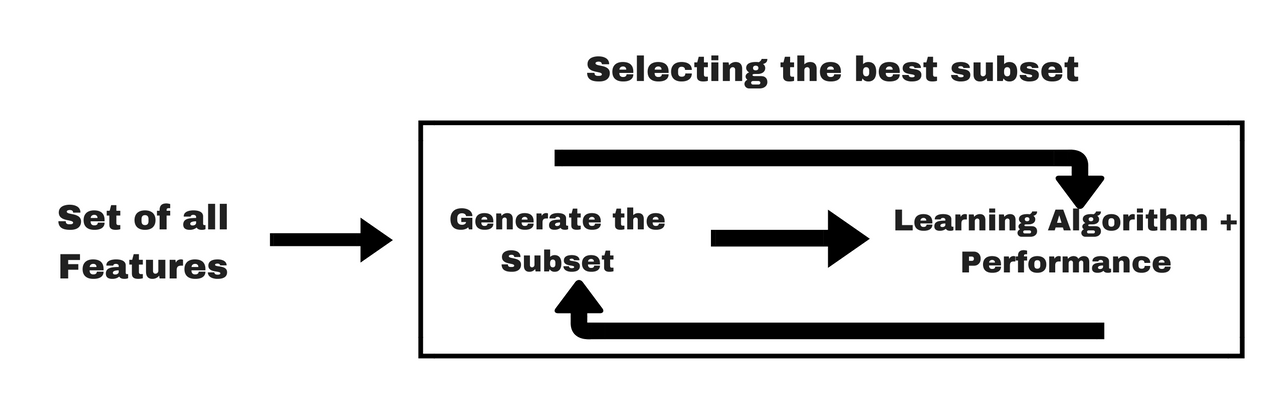
Metody osadzone wykorzystują algorytmy, które mają wbudowane metody wyboru funkcji. Metody te są iteracyjne. Chodzi o to, iż dbają o każdą iterację procesu uczenia modelu i starannie wyodrębniają te cechy, które najbardziej przyczyniają się do uczenia dla określonej iteracji.
Często metody osadzone wprowadzają dodatkowe ograniczenia do optymalizacji algorytmu predykcyjnego, który skłania model w kierunku mniejszej złożoności (mniej współczynników).
Najpopularniejszymi przykładami tych metod są regresja LASSO i las losowy, które mają wbudowane funkcje wyboru cech.
 https://www.analyticsvidhya.com
https://www.analyticsvidhya.comC. Oparte na wrapperach (Wrapper methods)
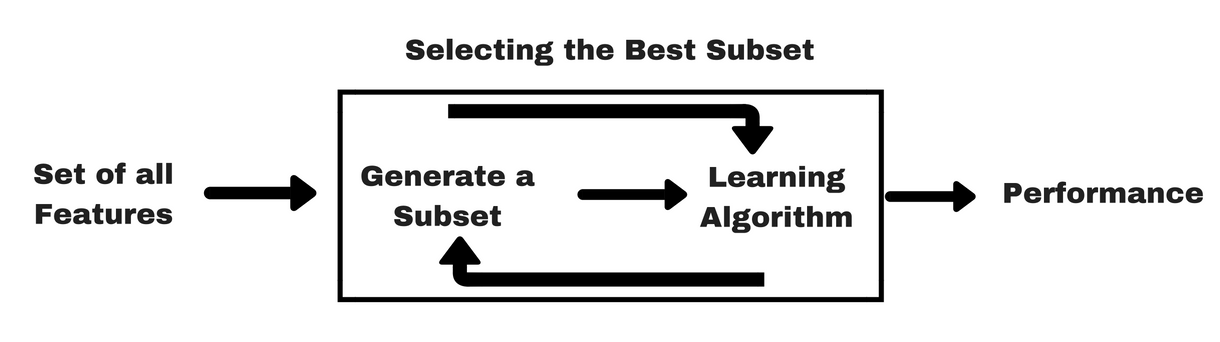
Są to metody, które traktują wybór zmiennych jako problem wyszukania. Proces wyboru cech opiera się na określonym algorytmie uczenia maszynowego, który staramy się dopasować do danego zbioru danych szukając optymalnego zestawu cech.
Na podstawie wniosków wyciągniętych z poprzedniego modelu decydujemy o dodaniu lub usunięciu funkcji z podzbioru. Może to być na przykład rekursywna eliminacja cech. Metody te są zwykle bardzo kosztowne obliczeniowo.
 https://www.analyticsvidhya.com
https://www.analyticsvidhya.comD. Metody hybrydowe (hybrid methods)
Są to po prostu metody, które łączą kilka wcześniej opisanych.
Jestem przekonany, iż jeżeli przeczytasz poniższe metody, to zainspirujesz się i sam/sama stworzysz własne rozwiązanie hybrydowe!
Która metoda jest najlepsza?
Jeśli zobaczysz artykuł, gdzie będzie informacja o najlepszej metodzie do wszystkich problemów, to … uciekaj!
Nie ma najlepszej metody wyboru funkcji.

Tak jak nie ma najlepszego zestawu zmiennych wejściowych ani najlepszego algorytmu uczenia maszynowego. Zamiast tego musisz odkryć, co najlepiej sprawdza się w Twoim konkretnym problemie, używając wielu eksperymentów.
Wypróbuj kilka metod selekcji zmiennych aby odkryć, co najlepiej sprawdza się w przypadku Twojego konkretnego problemu. Wraz z doświadczeniem i kolejnymi projektami zdobędziesz lepszą intuicję.
Eksperyment!
Nie jestem zwolennikiem samej teorii. Zatem przedstawię Ci wszystkie metody na jednym i tym samym przykładzie danych, abyś zobaczył, jak można zastosować je w praktyce.

Kwartał temu opuściłem mój ukochany polski bank Santander, w którym miałem okazję stawiać pierwsze kroki i poznawać świat AI oraz uczenia maszynowego. Z przyjemnością posłużę się danymi, które Santander opublikował na Kaggle. Dane możesz pobrać TUTAJ.
Jest to zbiór danych zawierający dużą liczbę zmiennych numerycznych. Kolumna „TARGET” to zmienna do przewidzenia – jest równa 1 dla niezadowolonych klientów i 0 dla zadowolonych klientów. Przyjrzyjmy mu się bliżej.
Wczytanie i przygotowanie danych

Jak widzisz podaję od razu biblioteki, których użyłem, aby ułatwić Ci powtórzenie eksperymentu.

Mamy sporo danych. Traktuję je jako eksperyment do pokazania Ci najróżniejszych metod. W związku z tym, aby przyśpieszyć wyliczenia, przygotuję mniejszy zbalansowany zbiór danych w podziale na:
- zbiór treningowy – będę na nim wybierał cechy, a następnie trenował modele dla mniejszego zestawu cech,
- zbiór testowy – za jego pomocą będę ostatecznie sprawdzał predykcję.

Model podstawowy
Na początku zbudujmy model podstawowy na wszystkich cechach. Będzie służył nam do porównania, o ile nam spadła lub wzrosła moc modelu zbudowanego na podstawie 369 zmiennych!
Aby wyniki były porównywalne, będę wykorzystywał bardzo prosty zestaw hiperparametrów. Bibliotekę pomocniczą utils, gdzie umieściłem kilka funkcji pomocniczych do przeliczenia metryk, możesz pobrać TUTAJ.

Dane są zbalansowane (po 50% dla obu klas), więc wszystkie metryki są intuicyjne.

Normalizacja
Niektóre z użytych metod będą wymagać, aby dane były nieujemne i najlepiej znormalizowane. Dlatego wykorzystajmy proste metody zaszyte w sklearn.
a następnie przeliczmy jeszcze raz model:

W tym przypadku operacja była bez wpływu na moc modelu.
Uwaga! Zauważ, iż korzystając z StandardScaler i MinMaxScaler skorzystałem z funkcji fit_transform na zbiorze treningowym, a tylko z transform na zbiorze testowym. Chodzi o to, iż zbiór testowy traktujemy jakby to były nowe dane produkcyjne i nigdy nie możemy na nim nic trenować.
Dobrze, mamy sporo zmiennych w modelu – aż 369. Pewnie nie trzeba wykorzystywać wszystkich zmiennych do przewidywania klientów. Popatrz, jakich metod możemy użyć.

A. Feature selection – metody oparte na filtrach
Zacznijmy od najprostszych, ale często również dość skutecznych metod. Warto jednak podkreślić, iż te najprostsze metody powinny głównie posłużyć do nie do wyboru najlepszych zmiennych, a głównie do odrzucenia tych kiepskich.
1. Variance Threshold (próg wariancji)
Cechy stałe to takie, które wykazują tylko jedną wartość dla wszystkich obserwacji zbioru danych. To jest ta sama wartość dla wszystkich wierszy zestawu danych. Te funkcje nie dostarczają żadnych informacji, które umożliwiają modelowi uczenia maszynowego rozróżnianie lub przewidywanie celu.
I tutaj z pomocą przychodzi nam próg wariancji, który jest prostym i podstawowym podejściem do wyboru cech. Usuwa wszystkie cechy, których wariancja nie osiąga pewnego zadanego progu. Implementacja w sklearn domyślnie usuwa wszystkie cechy o zerowej wariancji, tj. cechy, które mają taką samą wartość we wszystkich próbkach. Zakładamy, iż cechy o większej wariancji mogą zawierać więcej przydatnych informacji, ale zauważmy, iż nie bierzemy pod uwagę związku między zmiennymi cech lub zmiennymi cech a zmiennymi docelowymi, co jest jedną z wad metod filtrowania.
Dodajmy jeszcze funkcje do przeliczenia podstawowego modelu na mniejszym zbiorze danych

Wow. 200 cech mniej a metryki takie same.
Ale spokojnie, to dopiero początek. Jestem przekonany, iż uda nam się ten wynik przebić. A wiesz dlaczego? Bo na pewno są tam jeszcze zmienne, które są szumem i zaburzają możliwość nauki modelu.
Aby kolejnym metodom ułatwić ich zadanie zapiszmy sobie te 171 zmiennych i będą one dla nas punktem wyjściowym w kolejnych metodach.

Uwaga! Podobnie może być z cechami, które uzupełnione są dla mniej niż np. 1% populacji. Choć tutaj warto zapoznać się z wiedzą domenową! Dlatego powinniśmy być ostrożni przy usuwaniu tego typu funkcji i najlepiej przedyskutować wątpliwości z ekspertem domenowym.
2. Chi squared (Chi kwadrat)
Ta metoda wyboru zmiennych polega na przetestowaniu związku między cechami w zbiorze danych a zmienną docelową. Obliczamy chi-kwadrat między każdą cechą a celem i wybieramy pożądaną liczbę cech z najlepszymi wynikami chi-kwadrat.
W teorii mówi się, iż test chi-kwadrat jest używany głównie dla cech kategorialnych w zbiorze danych. Natomiast w praktyce możesz także użyć go na danych, które mamy. Możecie sami sprawdzić, iż wynik jest ten sam zmieniając nasze dane (wartości miedzy 0 a 1) na kategoryczne. Na przykład podmieniając X_train na (10*X_train).astype(int).


Niestety sami podajemy parametr k (liczbę zmiennych). Ale to nie problem, zawsze można dodać pętle i zobaczyć krok po kroku jak będzie wzrastała moc modelu przy zwiększaniu liczby cech:

Ciekawy wynik. Zatem moglibyśmy dobrać z tej metody około 40 zmiennych. Mnie osobiście zainteresowałby ten mocny wzrost – pewnie to jest jedna z lepszych cech, którą mamy w zbiorze.
Hint! Przy wielu metodach możesz skorzystać z tego podejścia, aby wyliczyć kilka możliwości i optymalnie dobrać liczbę cech.
Dodatkowo, zamiast SelectKbest można wybrać na przykład SelectPercentile, który wybiera cechy zgodnie z percentylem najwyższych wyników.
3. ANOVA F-value For Feature Selection
W przypadku cech ilościowych możemy obliczyć wartość f-Anova między każdą cechą a wektorem docelowym. Wyniki wartości F sprawdzają, czy gdy grupujemy cechę liczbową według wektora docelowego, średnie dla każdej grupy są znacząco różne.


Tak jak poprzednio możemy zobaczyć jak to wygląda w przedziale wyboru od 1 do 100 cech:

4. Information gain (zysk informacji)
Zysk informacji oblicza zmniejszenie entropii z transformacji zbioru danych. Można go użyć do wyboru cech, oceniając zysk informacyjny każdej zmiennej w kontekście zmiennej docelowej. Zdobywanie informacji lub wzajemne informacje mierzą, jak obecność/brak danej cechy przyczynia się do prawidłowego przewidywania celu.
Information gain mierzy jak bardzo znajomość jednej zmiennej zmniejsza niepewność co do zmiennej przewidywanej. Na przykład, jeżeli waga i wzrost są niezależne, to znajomość wagi nie daje żadnych informacji o wzroście i odwrotnie. Ich wzajemne informacje wynoszą zero. Z drugiej strony, jeżeli informacje przekazywane przez wzrost są współdzielone z wagą, to wzajemna informacja jest taka sama jak niepewność zawarta w jednej ze zmiennych.


Bardzo interesujący wynik. W tym przypadku bardzo gwałtownie osiągamy wynik metryki f1 na poziomie 72%, a dokładając kolejne cechy zaczyna on się zmniejszać.
5. Correlation Coefficient (współczynnik korelacji)
Logika stojąca za wykorzystaniem korelacji do wyboru cech polega na tym, iż dobre zmienne są silnie skorelowane ze zmienną prognozowaną. Dodatkowo, w przypadku niektórych metod takich jak regresja logistyczna, warto zadbać, aby cechy nie były skorelowane z innymi cechami.

Oczywiście zmienna sama ze sobą wszystko wyjaśnia i wówczas korelacja przyjmuje wartość 1. Jak w powyższym przykładzie zmienna „TARGET” sama ze sobą daje taką wartość.

I tak jak wspomniałem powyżej, można użyć tej metody do usunięcia zmiennych skorelowanych samych ze sobą:

6. Fisher score
Skala Fishera jest metodą chętnie wykorzystywaną do selekcji cech. Oblicza statystyki chi-kwadrat między każdą nieujemną cechą i klasą. Algorytm, którego użyjemy, zwraca rangę zmiennej na podstawie wyniku Fisher’a w kolejności malejącej. Następnie możemy wybrać zmienne zgodnie z rangą.


7. Information Value (IV)
Mam sentyment do tej metryki. Od kiedy zacząłem pracę w bankowości w 2008 roku przez kolejną dekadę służyła osobom budującym modele predykcyjne dotyczące ryzyka jako główna metryka mówiąca o mocy danej cechy.
Wartość informacyjna (IV) jest użyteczną techniką wyboru ważnych zmiennych, która pomaga uszeregować zmienne na podstawie ich ważności. Opowiem o niej więcej przy okazji artykułu o regresji logistycznej i modelowaniu ryzyka kredytowego, który planuje napisać w najbliższym czasie.
Ogólna zasada jest taka, iż jeżeli IV jest:
- < 0,02 – cecha nie jest przydatna do modelowania,
- 0,02 do 0,1 – zmienna ma tylko słabą relację z ilorazem szans dobra/złe,
- 0,1 do 0,3 – predyktor ma średnią relację siły do ilorazu szans dobra/złe,
- 0,3 do 0,75 – wtedy predyktor ma silny związek ze stosunkiem szans dobra/złe,
- > 0,75 bardzo mocna i warto sprawdzić czy nie jest to jakaś zmienna wróżka (data leak)!



B. Feature selection – metody oparte
na osadzeniach
8. Lasso Regularization (regularyzacja Lasso)
Regularyzacja polega na dodaniu kary do różnych parametrów modelu uczenia maszynowego w celu zmniejszenia swobody modelu, tj. uniknięcia nadmiernego dopasowania. W regularyzacji modelu liniowego kara jest nakładana na współczynniki, które mnożą każdy z predyktorów. Z różnych typów regularyzacji, Lasso lub L1 ma adekwatność, która jest w stanie zmniejszyć niektóre współczynniki do zera. Dlatego tę funkcję można usunąć z modelu.
Techniki regularyzacji pomagają zmniejszyć ryzyko nadmiernego dopasowania i pomagają nam uzyskać optymalny model. Regularyzację można wykorzystać na dziesiątki sposobów. Jednym z nich jest wykorzystanie regularyzacji Lasso do nakładania kar na współczynniki, co powoduje zerowanie zmiennych w modelu.

9. Random Forest Importance
Lasy losowe to jeden z najpopularniejszych algorytmów uczenia maszynowego. Są bardzo skuteczne, ponieważ zapewniają ogólnie dobrą wydajność predykcyjną, niski overfitting i łatwą interpretację istotności zmiennych. Innymi słowy, łatwo jest obliczyć, w jakim stopniu każda zmienna przyczynia się do podjęcia decyzji.
Lasy losowe składają się z dziesiątek, setek lub tysięcy drzew decyzyjnych, z których każde zbudowane jest na podstawie losowego wyboru obserwacji ze zbioru danych i losowej ilości zmiennych. Żadne drzewo nie widzi wszystkich danych i cech, co gwarantuje, iż drzewa są mniej podatne na nadmierne dopasowanie.
Każde drzewo jest również sekwencją pytań tak-nie opartych na jednej zmiennej, np. „czy klient zarabia mniej niż 5.000 pln?”. W każdym pytaniu (węźle drzewa) dzielą zbiór danych na 2 segmenty, z których każdy zawiera obserwacje, które są między sobą bardziej podobne i różnią się od tych z drugiego segmentu. W przypadku klasyfikacji miarą zanieczyszczenia jest zanieczyszczenie Giniego lub entropia. Dlatego podczas trenowania drzewa można obliczyć, o ile każda cecha zmniejsza zanieczyszczenie. Im bardziej dana cecha zmniejsza zanieczyszczenie, tym ważniejsza jest to cecha. W lasach losowych spadek zanieczyszczenia z każdej cechy można uśrednić między drzewami, aby określić ostateczne znaczenie zmiennej.
Mówiąc prościej, zmienne wybrane na wierzchołkach drzew są ogólnie ważniejsze niż cechy wybrane na końcowych węzłach drzew. Dzieje się tak, ponieważ górne podziały prowadzą do większego przyrostu informacji.



C. Feature selection – metody oparte
na wrapperach
10. Forward Feature Selection
Idea metody jest bardzo prosta. Jest to metoda iteracyjna, w której zaczynamy od najlepiej działającej zmiennej względem celu. Następnie wybieramy kolejną zmienną, która daje najlepszą wydajność w połączeniu z pierwszą wybraną zmienną. Proces ten trwa aż do osiągnięcia zadanego kryterium.
Taki typ selekcji nazywamy również metodami zachłannymi, ponieważ oceniają wszystkie możliwe kombinacje pojedynczych, podwójnych, potrójnych i tak dalej cech. Dlatego jest dość kosztowna obliczeniowo!
W implementacji mlxtend jako kryterium zatrzymania jest arbitralnie ustawiona liczba cech. Tak więc wyszukiwanie zakończy się, gdy osiągniemy pożądaną liczbę wybranych funkcji. Ja ustawiłem parametr na „best”.
Dodatkowo specjalnie dałem o wiele mniejszy las losowy (tylko 10 estymatorów i głębokość 5) i ustawiłem parametr walidacji krzyżowej cv=2 w celu przyśpieszenia obliczeń. Zwróć uwagę, iż w tak prostym przypadku i przy tak małej liczbie obserwacji, obliczenia trwały 4 minuty.

W powyższym kodzie dodałem w Jupyter Notebook tzw. magiczną komendę %time, która dodatkowo zróciła informacje o czasie wykonywania.

11. Backward Feature Elimination
Ta metoda to tak jakby brat bliźniak powyższej metody. Działa dokładnie odwrotnie do metody Forward Feature Selection.
Zaczynamy od wszystkich zmiennych i budujemy model. Następnie usuwamy z listy cech zmienną, która daje najlepszą wartość miary oceny. Proces ten jest kontynuowany aż do osiągnięcia zadanego kryterium.


12. Exhausive Feature Selection
Jest to najbardziej zachłanny i kosztowny obliczeniowo algorytm z całej tej listy! Ponadto jest to typowe rozwiązanie „brute-force” – próbuje każdą możliwą kombinację zmiennych i zwraca najskuteczniejszy podzbiór.
Zatem, jeżeli chcemy zbudować model SVM i mamy zbiór składający się dla przykładu tylko z 4 cech (wiek, wzrost, waga, płeć), to algorytm przetestuje model na zbiorze 15 kombinacji:
- 1 zmiennej: np. wiek,
- 2 zmiennych, np. wiek+płeć,
- 3 zmiennych, np. wiek+wzrost+płeć,
- 4 zmiennych: wiek+wzrost+waga+płeć,
i wybierze tę kombinację zmiennych, która zapewnia najlepszą wydajność (np. dokładność klasyfikacji) dla wybranego modelu.
Niestety mój komputer nie chciał w miarę szybkim czasie przeliczyć zbiorów powyżej kilku cech Dlatego poniżej przykład z wybraniem do 2 zmiennych.

13. Recursive Feature Elimination
Jest to kolejny zachłanny algorytm optymalizacji, którego celem jest wybieranie cech poprzez rekurencyjne uwzględnianie coraz mniejszych zestawów cech.
Metoda RFE wielokrotnie tworzy modele i odkłada na bok najlepszą lub najgorszą funkcję w każdej iteracji. Konstruuje następny model z pozostałymi cechami, aż wszystkie cechy zostaną wyczerpane. Następnie klasyfikuje cechy na podstawie kolejności ich eliminacji.


W najgorszym przypadku, jeżeli zbiór danych zawiera N cech, RFE wykona chciwe wyszukiwanie 2N kombinacji cech.
14. Recursive Feature Elimination with Cross Validation
Jest to kolejna metoda z sklearn. Metoda ta jest modyfikacją wcześniejszej metody poprzez dodanie do niej techniki walidacji krzyżowej.


D. Feature selection – metody hybrydowe
15. Random Forest Importance + random values
Wcześniej opisałem metodę lasu losowego. Tam na wyjściu dostaliśmy listę zmiennych poszeregowanych od najbardziej istotnych cech do mniej istotnych.
Do tej metody zacząłem używać pewnej sztuczki:
- do mojej listy zmiennych dodaję nowe stworzone zmienne, które są losowymi zmiennymi (np. 20 takich nowych cech),
- buduję model lasu losowego na tym rozszerzonym zbiorze danych,
- wyliczam średnią moc (importance) na zmiennych losowych,
- wybieram tylko te cechy, których importance jest powyżej wartości z punktu 3.
Dzięki temu bardzo gwałtownie otrzymuję fajną listę cech, które wnoszą coś dodatkowego do modelu.

16. Boosting + Shap + Forward group selection
A tutaj inna metoda, którą zacząłem stosować w ubiegłym roku i która daje mi często bardzo zadowalające wyniki. Czas wyliczeń jest dłuższy niż wcześniejsza metoda, ale fajnie mieć alternatywę.
Sposób działania wygląda tak:
- wybieram któryś z modeli opartych na boostingu (np. XGBoost, LightGBM lub CatBoost),
- buduję model,
- wyliczam moc cech uszeregowanych dzięki wartości shapley’a,
- tworzę zbiór ze zmiennymi szeregując od najmocniejszych do najsłabszych,
- buduję kolejne modele biorąc top X kolejnych zmiennych tak długo, aż po dodaniu kolejnych zmiennych nie widzę wzrostu mocy modelu.



Podsumowanie
Uff… dobrnęliśmy do końca. jeżeli jesteś tutaj, to gratuluję Ci przejścia przez wszystkie metody dla „feature selection”. Mam prośbę, jeżeli znasz metodę, której nie opisałem, to dopisz ją w komentarzu. Postaram się za jakiś czas wrócić do artykułu i dopisać kolejne inspiracje od Was – czytelników bloga!
Pozdrawiam serdecznie z całego serducha,

Obraz Gerd Altmann z Pixabay
