Matura z matematyki to dla wielu uczniów moment wielkiego stresu. Niestety jest przedmiotem obowiązkowym na egzaminie dojrzałości, więc choćby o ile nie wiążesz z tym przedmiotem swojej przyszłości i np. kierunku studiów musisz do niej podejść. Co można zrobić, aby ułatwić sobie zdanie matury z matematyki i nie tracić na egzaminie cennych punktów, zwłaszcza o ile mierzysz tylko minimalny próg 30%?
Znajomość "pewniaków maturalnych", skutecznie zwiększyć Twoje szanse na pozytywny wynik. Poniżej znajdziesz obszary i zagadnienia, na które warto zwrócić szczególną uwagę, bo zadania z nich niemal zawsze pojawiają się na maturze z matematyki. Ich opanowanie to w praktyce zawsze łatwe i szybkie punkty.
Matura z matematyki - poziom podstawowy





Przygotuj się do matury z matmy bez stresu! Opanuj cały materiał we własnym tempie, naucz się rozwiązywać typowe zadania pojawiające się w arkuszach maturalnych i zapomnij o poprawce! Dowiedz się więcej
Algebra
Algebra to bez wątpienia jeden z najważniejszych działów matematyki, który każdego roku pojawia się na maturze. Podstawy algebry, takie jak rozwiązywanie równań i nierówności, to podstawa. Ważne jest, aby powtórzyć różne metody rozwiązywania równań kwadratowych, zarówno przez deltę, jak i metodę wyłączania niewiadomej oraz rozkładania na czynniki. Ponadto, warto przypomnieć sobie zasady działania na wyrażeniach algebraicznych, w tym działania na ułamkach i potęgach.
Przykładowe zadania
1. Równania: Rozwiąż równanie x²−5x+6=0. Pamiętaj o metodzie delty oraz o rozkładzie na czynniki.
2. Równania i nierówności liniowe: Znajdź wszystkie wartości x, dla których 3x−7>5x+1. Tutaj najważniejsze jest przeniesienie niewiadomych na jedną stronę i liczb na drugą.
3. Ułamki: Uprość wyrażenie:
2x²-8 x²-4
i podaj warunki, dla których jest ono określone.
4. Równania wielomianowe: Znajdź wszystkie rozwiązania równania:
xł-6x²+11x-6=0.

Geometria
Geometria płaska, a w szczególności zadania dotyczące trójkątów, kwadratów, prostokątów oraz okręgów, regularnie pojawiają się na maturalnych arkuszach. najważniejsze jest opanowanie wzorów na obliczanie pola i obwodu tych figur, a także znajomość twierdzeń, takich jak twierdzenie Pitagorasa czy twierdzenie Talesa. Nie zapomnij również o geometrii analitycznej, gdzie często pojawiają się zadania związane z równaniami okręgu i prostych na płaszczyźnie.
Przykładowe zadania:
- Trójkąty: Oblicz pole trójkąta równobocznego o boku 6 cm.
- Okręgi: Znajdź długość promienia okręgu wpisanego w kwadrat o boku 8 cm. najważniejsze jest tutaj wykorzystanie zależności między bokiem kwadratu a promieniem okręgu.
- Własności trójkątów: Wykaż, iż w trójkącie prostokątnym wysokość opuszczona z kąta prostego dzieli ten trójkąt na dwa trójkąty, które są podobne do trójkąta wyjściowego oraz do siebie nawzajem.
- Teoria cosinusów: Oblicz długość trzeciego boku trójkąta, znając długości dwóch boków oraz miarę kąta między nimi.
Matura z matematyki - poziom podstawowy





Przygotuj się do matury z matmy bez stresu! Opanuj cały materiał we własnym tempie, naucz się rozwiązywać typowe zadania pojawiające się w arkuszach maturalnych i zapomnij o poprawce! Dowiedz się więcej
Funkcje
Znienawidzone przez wielu maturzystów funkcje również niezwykle często jest sprawdzany na egzaminie maturalnym. najważniejsze będzie więc opanowanie podstawowych typów funkcji: liniowej, kwadratowej, wykładniczej oraz ich adekwatności. Warto znać też metody rysowania wykresów tych funkcji, rozumieć pojęcie dziedziny i zbioru wartości, a także umieć rozwiązywać równania i nierówności z wykorzystaniem funkcji.
Przykładowe zadania:
- Funkcja liniowa: Narysuj wykres funkcji y=2x−3 i określ jej miejsce zerowe.
- Funkcja kwadratowa: Wyznacz wierzchołek paraboli opisanej funkcją y=x²−4x+3.
- Funkcja odwrotna: Znajdź funkcję odwrotną do funkcji f(x)=2x+3 i określ jej dziedzinę oraz zbiór wartości.
- Funkcja wykładnicza: Rozwiąż równanie 2x+1=32.

Statystyka i prawdopodobieństwo
Zadania z zakresu statystyki i prawdopodobieństwa również często goszczą na maturalnych arkuszach. Ważne jest, aby powtórzyć podstawowe pojęcia statystyczne, takie jak średnia arytmetyczna, mediana, moda czy odchylenie standardowe. Nie mniej istotne jest zrozumienie podstawowych zasad rachunku prawdopodobieństwa, w tym kombinatoryki, która pozwala na obliczenie liczby możliwych kombinacji czy permutacji.
Przykładowe zadania:
- Statystyka: Oblicz średnią arytmetyczną i medianę dla ocen: 2, 3, 3, 4, 5, 6.
- Prawdopodobieństwo: Jaka jest szansa rzucenia co najmniej jednej "szóstki" przy trzech rzutach standardową sześcienną kostką do gry?
- Dystrybuanta: Dla danej funkcji dystrybuanty F(x), znajdź prawdopodobieństwo znalezienia się zmiennej losowej w przedziale [a,b].
- Permutacje: Na ile różnych sposobów można ustawić 5 książek na półce?
Matura z matematyki - poziom podstawowy





Przygotuj się do matury z matmy bez stresu! Opanuj cały materiał we własnym tempie, naucz się rozwiązywać typowe zadania pojawiające się w arkuszach maturalnych i zapomnij o poprawce! Dowiedz się więcej
Równania i układy równań
Równania i układy równań liniowych to w zasadzie co roku nieodzowna część matury z matematyki. Powinieneś więc opanować metody rozwiązywania układów równań, zarówno metodą podstawiania, jak i przeciwnych współczynników. Ponadto, umiejętność interpretacji graficznej układów równań może być bardzo pomocna przy rozwiązywaniu zadań maturalnych.
Przykładowe zadania:
1. Równania z parametrem: Dla jakich wartości parametru m równanie mx−4=0 ma dokładnie jedno rozwiązanie?
2. Równania logarytmiczne: Rozwiąż równanie log₂(x)+log₂(x-3)=2.
3. Równania z wartością bezwzględną: Rozwiąż równanie zawierające wartość bezwzględną ∣2x−3∣=7. Takie równania wymagają rozpatrzenia dwóch przypadków, w zależności od tego, czy wyrażenie wewnątrz wartości bezwzględnej jest dodatnie czy ujemne.
4. Równania wymierne: Równania, w których niewiadoma pojawia się w mianowniku, na przykład:
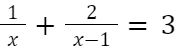
Rozwiązując takie równania, najważniejsze jest znalezienie wspólnego mianownika i rozpatrzenie dziedziny funkcji.
Przygotowanie do matury z matematyki na poziomie podstawowym wymaga skupienia się na różnorodnych typach zadań, w tym na tych prezentowanych w formie pytań wyboru, znanych jako zadania typu "ABC". Poniżej kilka przykładowych zadań, które mogą pojawić się na maturze jako "pewniaki" w takiej właśnie formie.
Zadanie 1: Funkcja liniowa
Funkcja liniowa f(x)=ax+b jest malejąca. Która z poniższych nierówności jest zawsze prawdziwa?
- a>0
- a
- b>0
- b 0 0
Zadanie 2: Twierdzenie Pitagorasa
W trójkącie prostokątnym długości boków są kolejnymi liczbami naturalnymi. Jaka jest długość najdłuższego boku tego trójkąta?
- 4
- 5
- 6
- 7
Zadanie 3: Prawdopodobieństwo
Rzucamy dwiema standardowymi kostkami do gry. Jakie jest prawdopodobieństwo, iż suma wyrzuconych oczek będzie równa 8?
- 5/36
- 1/6
- 1/12
- 1/18
Zadanie 4: Równania kwadratowe
Ile różnych rozwiązań ma równanie x²-4x+4=0
- 0
- 1
- 2
- Nieskończenie wiele
Zadanie 5: Procenty
Towar przed obniżką kosztował 200 zł. Po dwukrotnej obniżce ceny o 10%, jaka jest obecna cena towaru?
- 160 zł
- 162 zł
- 180 zł
- 184 zł
Zadanie 6: Geometria analityczna
Punkt A(3,−2) leży na prostej o równaniu:
- y = 2x−8
- y = −2x+7
- y = 1/2x-3
- y = -1/2x-1
Zadanie 7: Funkcja kwadratowa
Wierzchołek paraboli, będącej wykresem funkcji kwadratowej x²-6x+9, ma współrzędne:
- (3,0)
- (3,−9)
- (−3,9)
- (0,3)
Zadanie 8: Statystyka
Średnia arytmetyczna pięciu liczb: 2, 3, x, 4, 5 wynosi 4. Wartość x to:
- 2
- 6
- 8
- 10
Zadanie 9: Równania i nierówności
Rozwiązaniem nierówności 3x−5
- x
- x>3
- x
- x>4 43
Zadanie 10: Procenty i ułamki
Ile procent liczby 1/2 stanowi liczba 1/4?
- 25%
- 50%
- 75%
- 200%
Matura z matematyki - poziom podstawowy





Przygotuj się do matury z matmy bez stresu! Opanuj cały materiał we własnym tempie, naucz się rozwiązywać typowe zadania pojawiające się w arkuszach maturalnych i zapomnij o poprawce! Dowiedz się więcej
Podsumowanie
Znajomość "pewniaków maturalnych" to solidny fundament, ale pamiętaj, aby nie opierać się tylko na nich. Kluczem do sukcesu jest praktyka i zrozumienie. Rozwiązuj więc różnorodne zadania, aby zaznajomić się z możliwymi pułapkami i nauczyć się zarządzania czasem. Pamiętaj, iż matematyka to nie tylko liczby, ale także logiczne myślenie i umiejętność analizy problemów. Wierzymy, iż ten artykuł pomoże Ci przygotować się do maturalnego wyzwania i życzymy powodzenia na egzaminie!
2(x−1)>