Binarna klasyfikacja obrazów

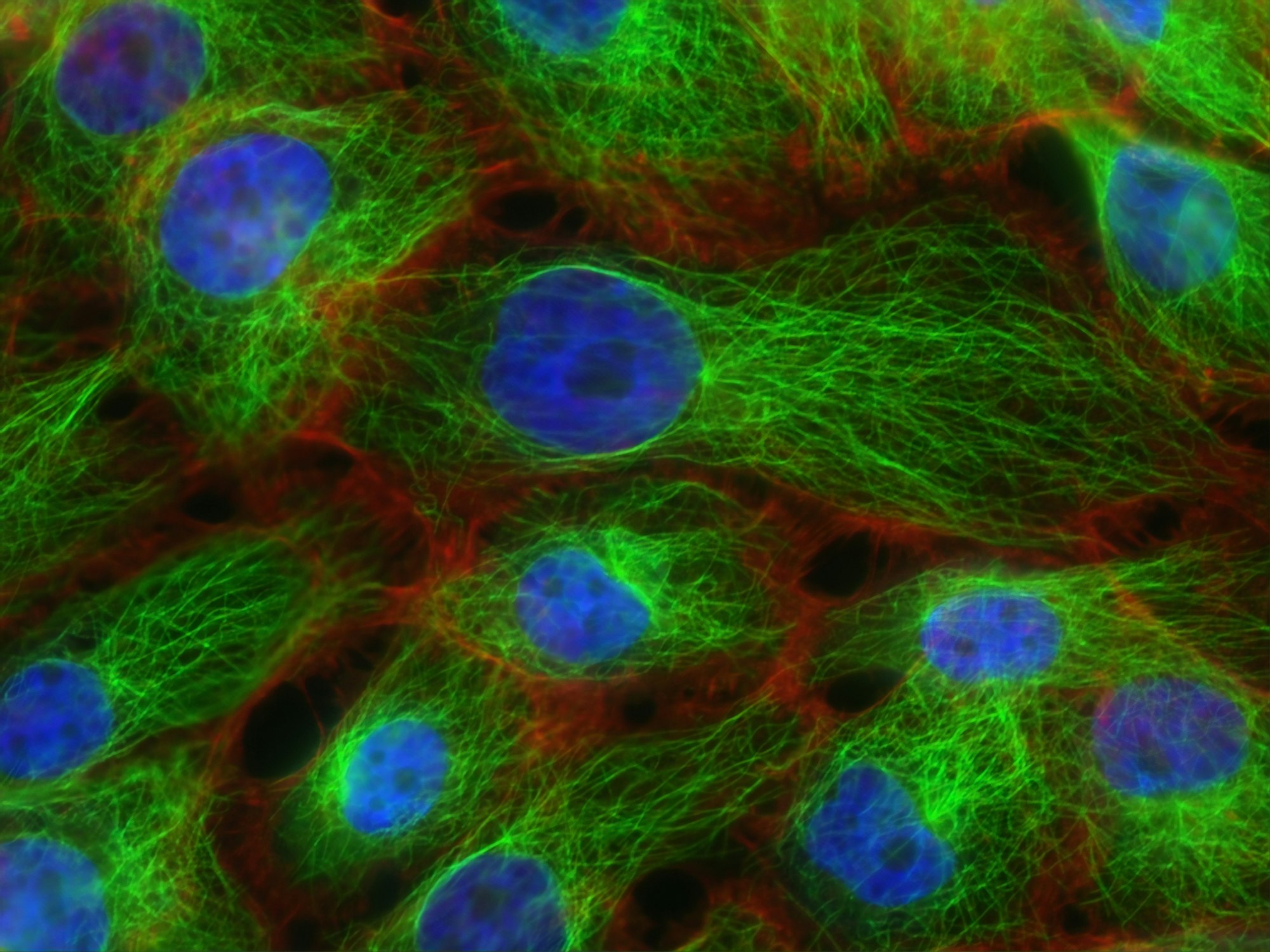
Ten post zawierać będzie wprowadzenie do trenowania modeli sieci neuronowych. Zajmiemy się tematem klasyfikacji binarnej, czyli rozpoznawaniem czy dany obraz należy do jednej z dwóch kategorii.

Będą to elementarne podstawy - kod, z którym można rozpocząć przygodę z trenowaniem modelu; bez wchodzenia w detale; ultra-prosty model, dający słaby wynik. Niemniej nie martw się, w przyszłych postach, budując wiedzę krok po kroku przejdziemy do bardziej wyszukanych rozwiązań.

Wiele 'tutorial-i' rozpoczyna klasyfikację od rozróżniania kotów i psów - ja pójdę zdecydowanie dalej. Zbiór danych, którego tutaj użyjemy to "skany histopatologiczne", czyli zajmiemy się próbą klasyfikacji czy dany skan komórek zawiera w części centralnej komórki rakowe.

[Ten post jest fragmentem serii "Krok po kroku" wprowadzającej do uczenia maszynowego (Machine Learning). Zapraszam do zapoznania się z całością.]

Która biblioteka ML?

Możnaby długo dywagować która biblioteka jest 'najlepsza' i 'najlepsze do czego'... Patrząc na biblioteki, z którymi pracowałem idealną na potrzeby rozpoczęcia przygody z uczeniem maszynowym w Computer Vision jest Keras.

Główną zaletą jest mała ilość kody, jaką trzeba napisać, aby "dojść do celu".

Instalacja biblioteki Keras

Keras jest w tej chwili częścią bardziej rozbudowanego frameworka od Google : TensorFlow. I właśnie instaluje się ją poprzez ten drugi - celem instalacji w linii komend należy wpisać:

pip install tensorflow==2.1.0

Wpisałem jawnie wersję, gdyż kompatybilność wersji jest różna. Ja tworząc ten kod używałem 2.1 i mam 100%-tową pewność, iż przykłady działają.

Przygotowanie danych

Wczytanie danych z plików datasetu to sprawa wyboru adekwatnych bibliotek do formatów danych. Dokładny opis wczytania zbioru można znaleźć tutaj.

Funkcja wczytująca dane i jej wywołanie

Ze względu na to, iż jest to wprowadzenie, wykonamy trening jedynie na jednym podzbiorze (train). Rozważanie na temat jak używać innych części zbioru będą tematami innych postów.

Materializacja danych (konwersja do tablicy numpy)

Definicja modelu

Najprostszy model sieci neuronowej składa się z warstw neuronów połączonych ze sobą sekwencyjnie.

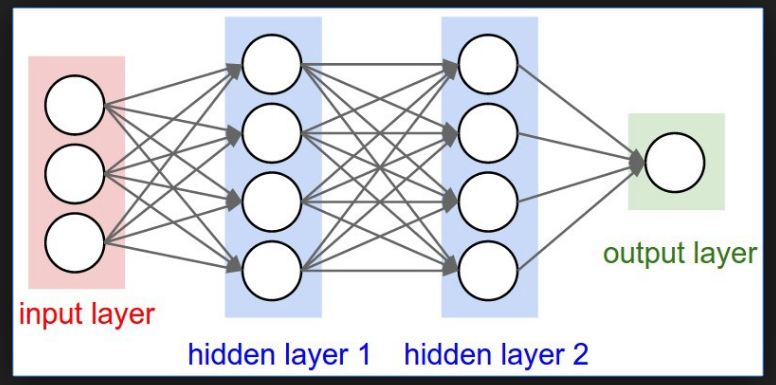Wizualizacja koncepcji budowy sieci neuronowej

Nie będziemy teraz zajmować się technicznymi aspektami operacji matematycznych jakie wykonują się wewnątrz sieci. Zamiast tego przystapny do budowy takiej konfiguracji w Keras-ie:

import tensorflow as tf import tensorflow.keras as keras # Model definition model = keras.models.Sequential() model.add(keras.layers.Cropping2D(32, input_shape= [96,96,3])) model.add(keras.layers.Flatten()) model.add(keras.layers.Dense(8, activation='relu')) model.add(keras.layers.Dense(1, activation='sigmoid'))

W powyższym przykładzie umieściłem 4 warstwy. Dwie w pełni połączone (Dense - takie, jak warstwy na schemacie koncepcji budowy sieci) oraz dwie dodatkowe o specjalnych zadaniach.

Warstwa Cropping2D odcina marginesy o szerokości 32 (czyli zostaje 32x32). Dlaczego? Dataset dostarczony jest z oznakowaniem występowania komórek rakowych dokładnie w tym regionie.

Warstwa Flatten konwertuje obraz będący dwuwymiarowy do płaskiego wektora (tablicy jednowymiarowej).

Wnikliwe oko dostrzeże, iż warstwy Dense opatrzone są różną funkcją aktywacji (ReLU/Sigmoid). Ale o tych szczegółach innym razem...

Przygotowanie treningu

Aby przeprowadzić trening, oprócz definicji sieci wymagane jest określenia parametrów uczenia.

Pierwszym parametrem jest wybranie funkcji kosztu (zwana też: funkcją straty). Na chwilę obecną przyjmijmy a priori iż "binary crossentropy" (binarna entropia krzyżowa) jest adekwatną funkcją kosztu dla zadania nauki klasyfikacji o dwóch kategoriach. W innych postach postaram się opisać co to adekwatnie jest :)

Drugim parametrem jest określenie algorytmu optymalizacyjnego. W ramach pokazywania sieci kolejnych obrazów chcemy aby jej parametry (wagi) były modyfikowane tak, aby coraz lepiej realizowała funkcję kosztu. Po każdym batchu danych (porcji danych) optymalizator zmienia wagi według określonych reguł. Na początek użyjemy SGD (Stochastic Gradient Descent).

Jako opcjonalny dodatek wskażę również metrykę accuracy (celność) by w sposób intuicyjny móc określić jakość wytrenowanego modelu.

Kod:

optimizer = keras.optimizers.SGD(learning_rate=1e-5) model.compile(optimizer=optimizer, loss='binary_crossentropy', metrics=['accuracy'])

Trening

Podstawowe wywołanie funkcji treningu w Keras jest banalnie proste:

fit_result = model.fit(x, y, batch_size=4, epochs=150)

Epoką nazywamy czas, w którym sieć zobaczyła wszystkie obrazy wejściowe. Ustawiając wartość na 150 wiem, iż każdy przypadek będzie użyty 150-ciokrotnie. Domyślnie, co epokę dane są mieszane i w każdej epoce sieć "widzi je" w innej, wylosowanej kolejności.

Analiza wyników

Po 150 epokach uzyskany wynik to : Accuracy (celność) = 65.27%. Jest to wynik bardzo słaby, ale dokładnie odpowiada skomplikowaniu użytego modelu. W przyszłych postach zobaczymy jak można ten wynik znacząco poprawić.

Ostatnie epoki nauki

Używając kodu do wizualizacji progresu nauki w ramach przechodzenia przez epoki:

import matplotlib.pyplot as plt plt.plot(fit_result.history['loss'], label='loss') plt.plot(fit_result.history['acc'], label='accuracy') plt.legend()

otrzymać można:

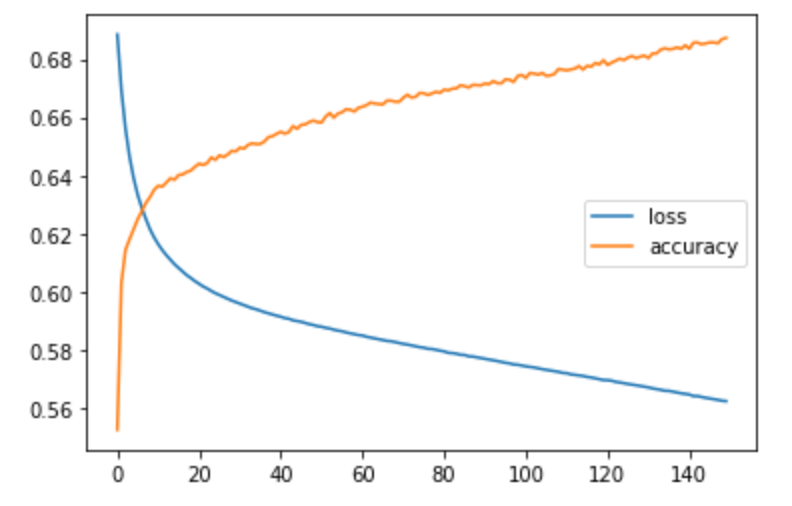
Wydaje się, iż zwiększając liczbę epok można by polepszyć wynik. Nie sprawdzamy jednak czy nie dokonujemy przeuczenia modelu, co może sprawiać, iż wynik jest zdecydowanie gorszy na danych spoza zbioru uczącego. Sprawdzimy to w następnych postach.

Uwaga poboczna: Po zwiększeniu ilości warstw wynik na zbiorze testowym może się poprawić. Przykład sieci:

Więcej warstw do klasyfikacji

Wynik osiąga po 150 epokach (na zbiorze treningowym) celność 72%.

Użycie wyuczonego modelu

Aby skorzystać z dobrodziejstw wyuczonego modelu używamy funkcji predict, bu poznać wyniki:

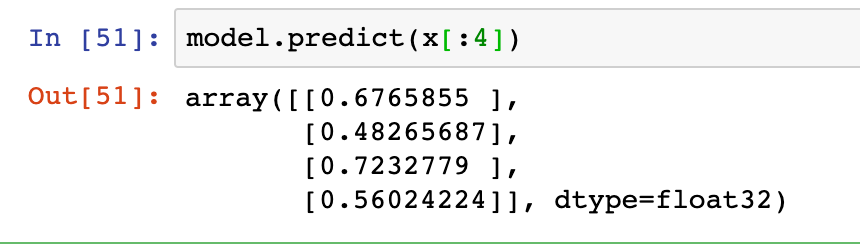
W powyższym przykładzie wziąłem dla przykładu 4 pierwsze obrazy ze zbioru treningowego. Zwracane wyniki można traktować jako prawdopodobieństwo przynależności do klasy - w najprostszym, choć nie jedynym ,wariancie: wartości poniżej 0.5 interpretować jako pozbawione komórek rakowych, te powyżej 0.5 przeciwnie.

Przy bieżącej skuteczności modelu nie można za bardzo ufać tym wynikom.
Aby zobaczyć jak to gwałtownie i równie proście ulepszyć powyższe rozwiązanie zapraszam do przyszłych postów.